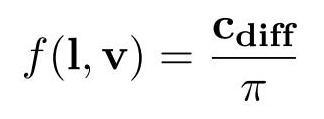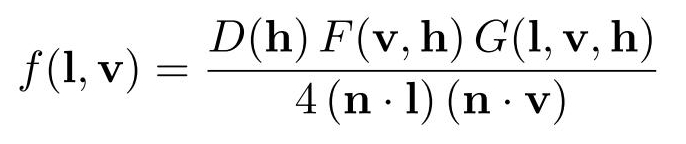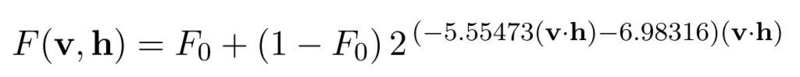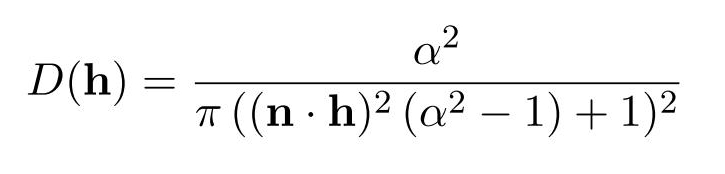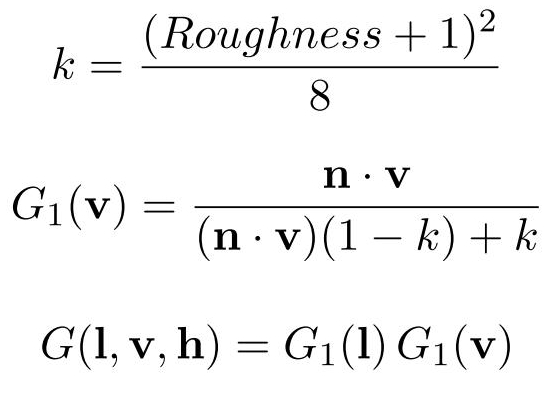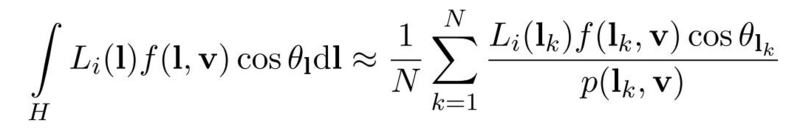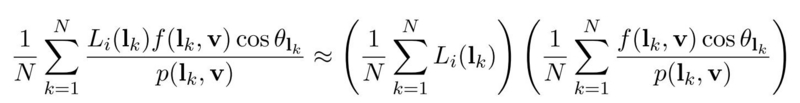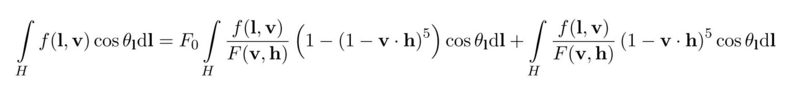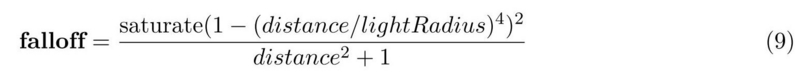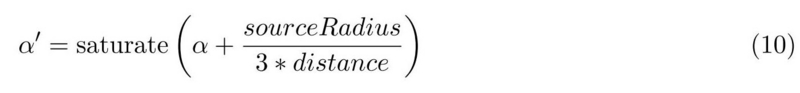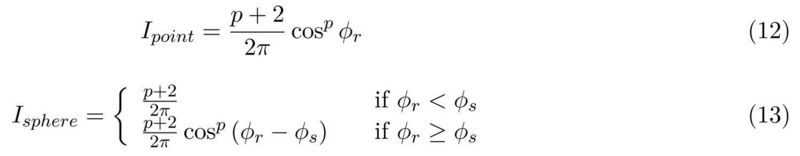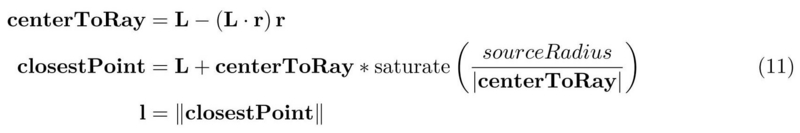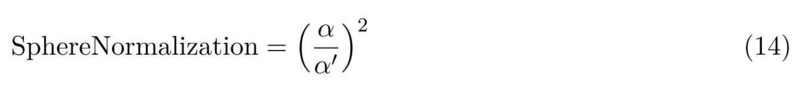"Unreal Engine4 のリアルシェーディング" (SIGGRAPH 2013)の説明

概要

  • 以前に軽く Unreal Engine4(アンリアルエンジン4)のシェーディングについて説明しました. (http://d.hatena.ne.jp/hanecci/20130719)
  • これに関連して SIGGRAPH 2013 でより完全な資料が公開されましたので, この記事では "Real Shading in Unreal Engine 4" SIGGRAPH 2013 について説明します.


参考文献

要旨

  • Unreal Engine4 で物理ベースなシェーディングをどう実装したか? についてで, 以下のような項目が紹介されています.
    • 物理ベースなディフューズとスペキュラのシェーディングの実装
    • スペキュラの IBL の実装
    • 複数のマテリアルを低コストでブレンドするためのレイヤーリングの仕組み
    • エリアライト(球状, カプセル状)の実装

個人的な感想

  • 流行(?)の物理ベースなシェーディングを, ゲーム向けにパフォーマンスも意識して実用的な範囲に落とし込んできている, という印象を受けました.
  • あと, アーティストが実作業でアセットを作っていくこともきちんと重視していることが好印象でした.

コンセプト

  • パフォーマンスの側面
    • (ゲームなので) パフォーマンスが重要で, 沢山のライトを扱える必要があります.
    • Unreal Engine4 でのレンダリングは Deferred Shading なので, GPU 負荷を減らすために G-Buffer に書き込むパラメータを減らしたいです.
    • マスクを使った複数のマテリアルのレイヤリングをサポートしたいけど, 複数回シェーディングする余裕はないので計算がリニアになってほしいです. つまり, 「複数のパラメータをブレンドしたシェーディング結果」= 「複数のシェーディング結果をブレンドしたもの」 ということです.
  • アートの側面
    • 計算に基づくライト(エリアライトとか)と, IBL の両方を扱える必要があります.
    • アーティストが調整するパラメータの数も減らしたいです.
    • アーティストが直感的に設定しやすいパラメータにする. (物体の屈折率を設定するのはなし)
    • 他のスタジオは Unreal Engine4 でフォトリアリズムを目標にしないかもしれないので, NPR (Non-Photorealistic Rendering) ができる余地も残す必要があります.

ディフューズシェーディング

  • 通常通りの完全ランバート反射です. (下図の左側の緑色の球を参照)
  • Disney 映画のラフネスを考慮したディフューズシェーディングも試したのですが(下図の右側の緑色の球を参照), コストに対する見た目の効果が薄かったのでやめたらしいです.

  • BRDF である f(l,v) は以下のようになります. c_diff はマテリアルのディフューズアルベドのカラーです.


スペキュラシェーディング

  • いつもの Cook-Torrance でのマイクロファセットを考慮したスペキュラシェーディングです.
  • 以下は フレネル反射率 F(v,h), マイクロファセットの分布関数 D(h), 幾何減衰率 G(l,v,h) について説明していきます.

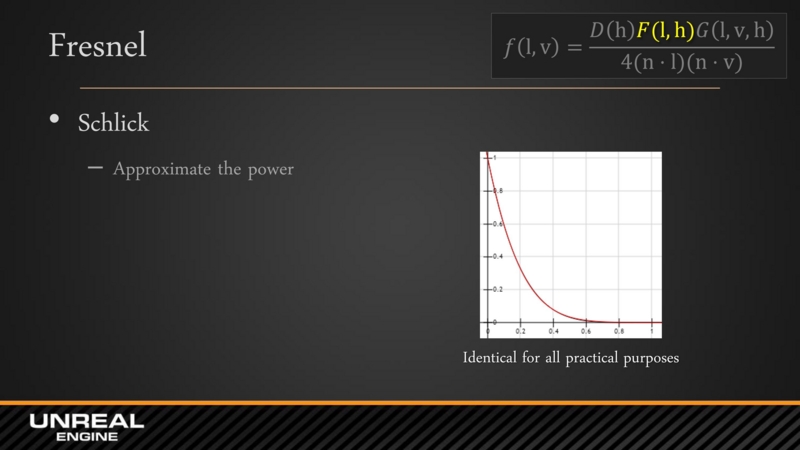
  • フレネル反射率 F(v,h)
    • 下図のスライドには Schlick 近似と書いてあります.


    • しかし, コースのノートを見ると見た目がほぼ同じだけど計算コストが低いフレネルのガウシアン球による近似である下図の数式を利用していると書いてありました.
    • ( Schlick 近似による計算の場合は計算に特殊関数である pow が入るため, GPU の特殊関数が処理できる計算ユニットを使う必要があるので ALU が増えやすいです. 一方で, ガウシアン球による近似の場合はdotと乗算なので, 全ての計算ユニットで処理できます. )


  • マイクロファセットの分布関数 D(h)
    • D(h) には Trowbridge-Reitz (GGX) を使っていました.
    • GGX は下図のようにスペキュラのハイライト部分がピーク部分以外にも残りやすい, という特徴を持っています.


    • GGX の数式は以下のようになります.


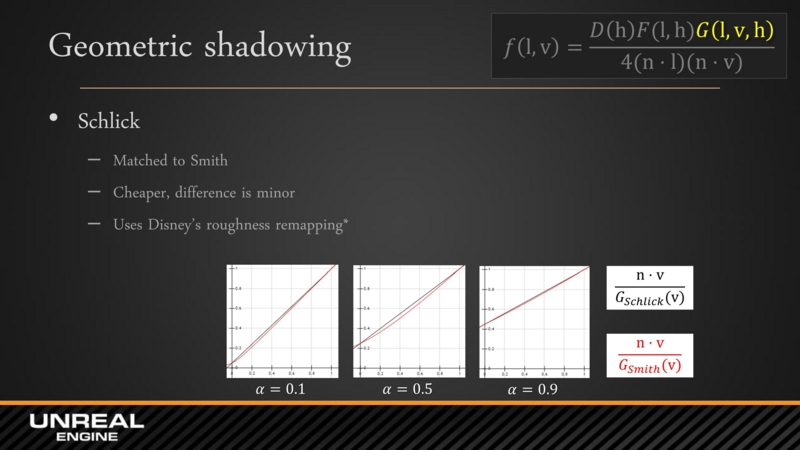
  • 幾何減衰率 G(l, v, h)
    • 幾何減衰率はマイクロファセットによる自己遮蔽によって生じるものなので, マイクロファセットの分布関数 D(m)と実は関連があります.
    • なので, ここでは見た目の向上に対して計算コストがそんなに高くないという理由で, Disney の方法と同様に GGX 用の幾何減衰率 G(l, v, h)を使っていました.


    • この GGX 用の幾何減衰率 G(l,v,h)については以下の数式です.

    • ラフネス0〜1をそのまま G(l,v,h)に使うとスペキュラが明るくなりすぎるという理由で Disney と同じ手法を使っていました.
    • つまり, ラフネス0〜1を一旦, 0.5〜1.0 にマッピングしています.
    • 数式0 については, 下の 数式2 に数式3 を代入し, 数式1 に数式2 を代入して整理すると, 数式0 になります.
    • このマッピング処理を行うのはポイントライトなどの計算するタイプの光源(Analytic light sources)に対してで, 一方でIBL 用の幾何減衰率については k = α/2 を使います.
k = (ラフネス + 1.0 )^2 / 8.0               [数式0]
k = α/2                                    [数式1]
α = (マッピングしたラフネス)^2             [数式2]
(マッピングしたラフネス)=(0.5 + ラフネス)/2 [数式3]

IBL のためのスペキュラシェーディングの近似計算

  • まず, ある点に対して半球状に光が入射して, 視点方向 v に跳ね返る放射輝度の計算式はいつものように下の左側のようになります.

  • さらに, これを下のように 2 つの項の乗算で近似します.

  • このとき, 1 項めの項を「環境マップの事前フィルタリング」とし, 2 項めの項を「環境 BRDF」とします.
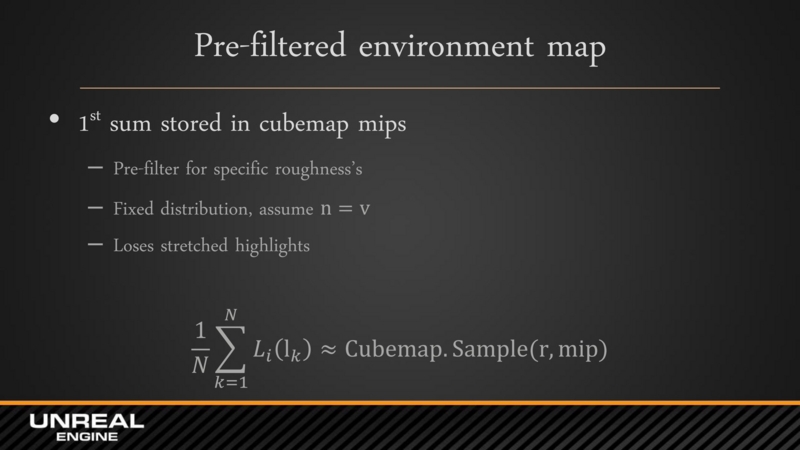
  • 1 項め: 「環境マップの事前フィルタリング」の計算方法


  • まずラフネスが完全に滑らかな場合, 完全な鏡面反射であるため視点ベクトルに対する 1 点の反射ベクトルを使って環境マップを 1 点だけサンプリングすれば良いです.
  • 一方で, もしラフネスが完全に粗い場合, ある 1 点に対して半球状の領域の範囲の環境マップを考慮する必要があります.
  • つまり, ラフネスに応じたスペキュラのシェーディングモデルのローブ(lobe)の変化によって, サンプリングする範囲(領域)が変化します.
  • 本来, この計算の結果はラフネスと視点ベクトルの両方に依存するのですが, 今回の例だと n = v = r として近似してしまい, 視点ベクトルには依存しないようにしています.
  • なので, 今回の場合だとラフネスに応じて, ある 1 点に入射する環境マップの平均値を求めれば良いことになります.
  • 実際の計算についてですが, ラフネスに応じた環境マップのサンプリングの範囲を求めるために, マイクロファセットの分布関数の D(h) である Trowbridge-Reitz (GGX)を使ってサンプリング範囲を求めています.
  • そして, ラフネスごとに求めたサンプリング範囲に基づいて環境マップのサンプリングを行い, その結果については環境マップの各ミップレベルに格納しています.
  • 具体的には, ラフネスが滑らかな面の場合は(高周波なので)高めの解像度のミップマップに入れています.
  • 一方で粗い面の場合は(低周波でぼやけるので), 低い解像度のミップマップに入れています.
  • 「環境マップの事前フィルタリング」のより詳しいコードの実装についてはコースノートの資料に載っているので, そちらを参照して下さい.
  • 2 項め: 「環境 BRDF」の事前計算
  • 次に 2 項めの環境 BRDF を計算については, フレネル計算の Schlick 近似である F(v,h) = F0 + ( 1 - F0 ) * ( 1 - v dot h )^5 を利用して, 下の数式のように BRDF の式を展開します.


  • そして, 上の数式を F0 * LUT.r + LUT.g とします.
  • LUT.r と LUT.g については事前計算して, 下図のようにテクスチャの U　方向 を cosθv, テクスチャの V 方向を ラフネスとした2 チャンネルのテクスチャに LUT テクスチャとして事前に計算しておきます.

  • 詳しいコードについてはコースのノートに載っているので, そちらを参照して下さい.
  • Environment BRDF については 3D LUT を使う方法もあるのですが, より最適化し コストを考慮して 2D LUT を使うことにしたそうです.
  • これは以前に紹介したように Killzone : Shadow Fall と同様な方法です.
  • 最後に IBL のスペキュラシェーディングの比較結果です.
  • (a) まず, 最初にきちんと重点サンプリングで計算したものが下図です.


  • (b) 次に「環境マップをサンプルする部分」と「環境 BRDF の部分」に分離して乗算する, という近似をした場合のものが下図です.


  • (c) 最後は 「環境マップの事前フィルタリング(視点方向に依存しないように n = v = r として近似)」した部分と, 「環境 BRDF」の部分に分離して乗算する, という近似をしたものです.


  • (a)(b)(c)を並べたものが下図で, (b)->(c)のときにラフネスが粗い右側部分に結構見た目の違いが出てしまっていますが, (a)とそれほど変わらないという理由でコストが低い (c)を使っています.


マテリアルのパラメータ

  • 現在の Unreal Engine4 のマテリアルのパラメータは下図のようにベースカラー, メタリック, ラフネス, キャビティの 4 種類です.

  • 以下にそれぞれのパラメータについて説明します.
  • ベースカラー
    • これはディフューズライティングとスペキュラライティングの両方の結果に影響していました.
    • なのでベースカラーはディフューズアルベドの役割だけでなく, スペキュラリフレクタンスとしての役割も果たしています.
  • メタリック
    • これはディフューズライティングとスペキュラライティングのリニア補間する割合だと思います.
    • 0.0 のときはディフューズライティングの結果になり, 1.0 のときはスペキュラライティングのみの結果になっていました.
    • 下図が(ベースカラーが黄色の)マテリアルのメタリックを変化させた場合の見た目の変化です.


  • ラフネス
    • これは従来通りのマイクロファセットによる表面の粗さを制御するもので, スペキュラシェーディングの結果のみに影響します.
    • 下図は金属(メタリック=1.0)のラフネスを変化させたときの見た目の変化です.

    • また下図は非金属(メタリック=0.0)のラフネスを変化させたときの見た目の変化です.


  • 下図が Unreal Engine 4 でのマテリアルパラメータの変遷( Samaritan デモ, Infiltrator デモ, 現在)です.

  • 最初の Samaritan デモのときはラフネスがなくて, 3種類のパラメータ(ディフューズカラー・スペキュラカラー・スペキュラパワー)を使っていました.
  • 次の Infiltrator デモのときに, Disney 映画の物理ベースなシェーディングを参考にして, 物理ベースのパラメータにがらっと置き換えて4種類のパラメータ(ベースカラー・メタリック・スペキュラ・ラフネス)を使っていました.
  • そして現在の Unreal Engine 4 になって, 上のスペキュラの代わりにキャビティが導入されています.
  • この 4 種類のマテリアルパラメータだけで表現力が足りそうなのか ? と思うかもしれないです. 実際は一部例外もあり, Epic Games が既に開発を進めていた Fornite については下図のように見た目が NPR なので, ベースカラーだけでは足りずに ディフューズアルベドカラーとスペキュラカラー(スペキュラリフレクタンス)を使っているそうです.

  • ただ Disney 映画の見た目も結構 NPR っぽいので, 結局は スペキュラカラーはなくても大丈夫かも, と書いてありました.

複数マテリアルのレイヤリング

  • Unreal Engine4 ではブレンド率を設定したマスクテクスチャによって, 2つのマテリアルをブレンドすることができます.
  • 下図は金属のマテリアルと, さびのマテリアルをブレンドした結果です.

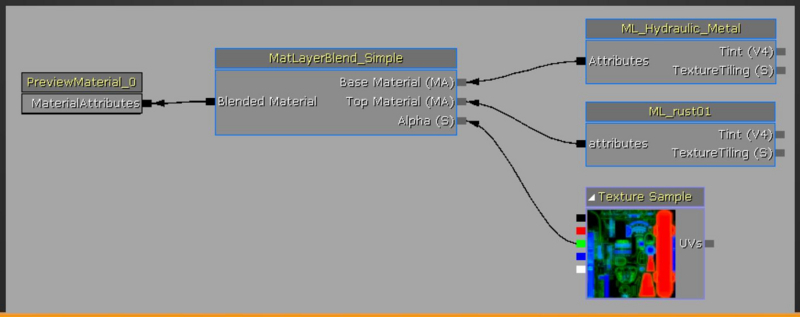
  • 複数マテリアルのレイヤリングに関する Unreal Engine4 でのシェーダノードの実装はシンプルで, 下図のように右上のマテリアルのノード 2 個と, 右下のブレンド率を設定したマスクテクスチャを用意してブレンドします.

  • 実際に GPU でこれらのブレンドを計算するときには, 各マテリアルごとにシェーディングした結果を混ぜると処理が重くなるので避けています.
  • その代わりに事前にマテリアルの基本パラメータをマスクテクスチャで混ぜてから, 1 回だけシェーディングしています.
  • これがうまくいくように, シェーディングの計算についてはリニアになるようにしているらしいです.
  • あと, 以下は複数のマテリアルのレイヤリングの機能を使った例です.


ライティングモデルの変更点

  • シェーディングモデルだけでなく, ライティングモデルもより物理的に正しいものに近づけようということで 2 つ新しい変更が行われました.
  • 1 つ目はライトの明るさの単位としてルーメン(lm)を導入しています.
  • 2 つ目はライトの輝度の減衰の仕方を距離の 2 乗に応じて減衰するものに変更しています.
  • 下図の左側が Unreal Engine の今までライトの減衰モデルで, 右側が今回の距離の 2 乗に応じて減衰するモデルです.

  • 左側の今までの減衰モデルだとライト付近の減衰が弱くて少し CG っぽい感じがしますが, 右側だと減衰の仕方が自然になった気がします.
  • ただ純粋に距離の 2 乗によって減衰するモデルだとライトによる影響が 0.0 になるのは距離が無限大のときです.
  • これだとゲームのパフォーマンスに影響して実用的に使えないので, ライトの影響半径(lightRadius)を定義しています.
  • そして, その値を使って下図のような数式で減衰を計算しています.

  • 分母の "+ 1" は距離が 0.0 になったときに分母が 0.0 になるのを防止するためのものです.

エリアライトの必要性

  • 物理ベースなシェーディングを行う場合には, ライトのスペキュラをより自然に見せるためにエリアライトを導入する必要があります.
  • 理由はもしエリアライトを使わない場合, ポイントライトのスペキュラのハイライトが小さくて不自然に見えることがあるからです.
    • 例えばポイントライトによるラフネスが滑らかな平面に対するスペキュラ反射は, ポイントライトのピークの点が 1 点だけなのでハイライトが非常に小さくなって不自然な見た目になってしまいます.
    • なので, こういう場合にはデザイナーさんは本当はラフネスが粗いマテリアルではないのだけれど, ラフネスを粗くしてハイライトをより大きくして自然に見せようとするという問題が起きるそうです.

"Specular D modification" (Epic Games, SIGGRAPH 2012)

  • 上の問題に対して Epic Games が SIGGRAPH 2012 で実装したエリアライトは, エリアライトの半径に応じてスペキュラシェーディング時のラフネスを変化させて, その結果ポイントライトのスペキュラシェーディングを擬似的にエリアライトのシェーディングのように見せることです.
  • これは "Specular D modification" と呼ばれています.
  • 具体的には以下の数式のように, エリアライトの半径(sourceRadius)や距離(distance)に応じて, 元々のラフネス(α)を擬似的にラフネス(α')と変化させて, エリアライトっぽく見せます.


  • 下図の左側が参照用の正しい結果で, 下図の右側がラフネスを擬似的に変化させてエリアライトっぽく見せた結果です.

  • しかし, 平面に対してかすめるような角度で見たり, ラフネスが粗めの場合はスフィアライトの形状が失われてしまっています.
  • あと, この方法はもし Blinn-Phong スペキュラのようにピーク付近に値が偏っている場合はこの方法でうまくいっていたらしいです.
  • しかし今回の GGX のようにピーク付近以外にも値が延びている場合だと, グロッシーなマテリアルにエリアライトのライティングが当たった場合に非常に粗い面に見えてしまう問題があるらしいです.

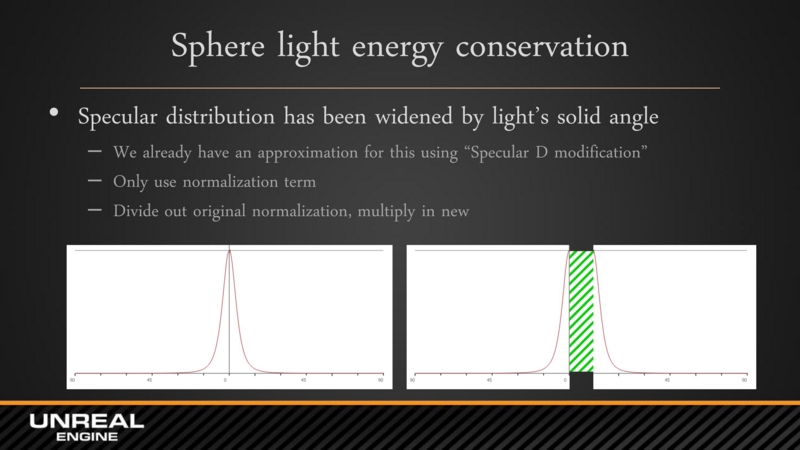
ポイントライトのピーク領域を広げて, スフィアライトとする

  • そこで今回の講演では, ポイントライトのピーク領域を広げてスフィアライトとする方法を導入していました.
  • 下図の (12) 式がポイントライトスペキュラライティングの式で, (13) 式が今回のスフィアライトの式です.


  • (12) 式についてはポイントライトのスペキュラライティングを 正規化 Phong shading で計算する場合のものです.
  • この場合, リフレクションベクトルとポイントライトの中心への方向ベクトル(正確にはシェーディング点からポイントライトへの中心ベクトル)がなす角度(Φr)によってピークの値からの減衰が発生します.
  • Φr = 0.0 のときはピークの値 ( p + 2 ) / 2PI になり, それ以外のときには (cosΦr)^p の減衰と ( p + 2 ) / 2PI の正規化が発生します.
  • (13)式のスフィアライトでは Φr=0.0 のとき以外にも, 反射ベクトルがスフィアライトにヒットする条件(Φr < Φs)のときにピーク値を取るようになっています.
  • またΦr >= Φs のときから, ( cos(Φr - Φs) )^p の減衰が発生します.
  • ここでの Φs はリフレクションベクトルとスフィアライトの近傍点( closestPoint )がなす角度です.
  • このスフィアライトの近傍点( closestPoint )については下の数式(11)で求めることができます.

  • 上の記号の意味については centerToRay : スフィアライトの中心からスフィアライトの表面の点のうちリフレクションベクトルに最近傍のものへ向かうベクトル, L:スフィアライトの中心へのベクトル, r:反射ベクトル, sourceRadius:スフィアライトの半径, です.
  • 下図の左側がポイントライトのスペキュラライティングのグラフで, 右側がピーク値をスフィアライトの半径分だけ引き伸ばしたグラフです.

  • ただピークの値の領域が増やす方法だとスフィアライトが放出するエネルギーの合計が増えてしまうという問題があります.
  • 従って, スフィアライトを正規化するための下の数式を追加して, 近似的にエネルギーが保存されるようにしています.

  • 上の数式でのαは元々のラフネスで, α'は "Specular D modification" で使っていたα'です.
  • 下図の左側が参照用の正しい結果で, 下図の右側が今回の手法の結果です.

  • エネルギー保存のための正規化の計算が近似的なものなので参照用と見た目が微妙に違いますが, 見た目が近いということで今回はこの手法を採用したらしいです.

チューブライト

  • またスフィアライトと別のタイプのエリアライトとして, 下図のようなチューブ状のライトも導入していました.


  • これの実装についてはコースのノートに数式入りで説明してありますので, 参照して下さい.

他の参考文献

Sony Pictures Imageworks のグローバルイルミネーションのレンダラー Arnold について

概要

  • この記事ではグローバルイルミネーションのレンダラーである Arnold について簡単に説明します.
  • Arnold は Sony Pictures Imageworks 社と Solid Angle SL 社によって共同開発されたレンダラーです.
  • 以下はArnold でレンダリングした CG 映画の場面です.



説明

    • Arnold は物理ベースなモンテカルロ法に基づくレイトレーサーです.
    • またフォトンマップやイラディアンスキャッシュというようにマルチパスによるキャッシュ計算はせずに, レイトレースによる単一パスから構成されます.
    • また視点方向からの単一方向のパストレーサーです.
    • 実装については C/C++ の最適化したコードからなっていて 200,000 行らしいです. またマルチスレッド対応, SIMD 対応です.
    • 最後に Arnold は Unbiased なレンダラーです. Unbias なレンダラーとはピクセルの輝度計算した結果の誤差が分散(統計学的な)にのみに依存します.
    • 輝度計算した結果の誤差(分散)を減らすには飛ばすレイのサンプル数を増やす必要があり, n 個のサンプル数によって √n だけ誤差が減ります.
    • Unbiased Rendering (Wikipedia English)
  • Arnold の長所
    • 1 パスのレンダリングになっていてシンプルです. (追加のファイルやキャッシュが不要です.)
    • レイのサンプル数というパラメータしかないので, シンプルです.
    • レイトレースのみでシャドウを計算するんで, シャドウマップが不要でシャドウの計算が完璧です.
    • 計算の品質をプログレッシブに改善可能です. (光源, シェーダ, カメラを動かした後に再計算で品質を改善できます.)
    • GI やライティング用にデータを保存しておく必要がないです.
  • Arnold の短所
    • マルチパスによる計算のキャッシュ化をしないので計算が重いかもしれませんが, そこは CPU が強力になること(マルチスレッド, CPU のマルチコア化)でカバーできることを前提にしています.
    • 1 パスでレンダリングするため, 幾何形状を常にメモリに載せておく必要があります.

参考文献